Popular Version of Paper S12.02
Presented Thursday, March 19, 1998
1998 APS March Meeting,
Los Angeles
In auditory and electrosensory neuronal systems, such as in certain owls and electric fish, there seems to exist an unresolved paradox [1]: They encode behaviorally relevant signals in the range of a few microseconds (a microsecond is one millionth of a second) with neurons that are ten to hundred times slower. The barn owl's auditory system is a prominent example that may serve to provide a solution [2] to the above paradox. The barn owl is a night hunter that localizes its prey in the dark through sound localization, i.e., by listening. Under normal circumstances, an adult owl needs six mice a night but once the youngsters, about five, have been hatched it has to catch a mouse every ten minutes - and it does so very successfully. Here we explain how and resolve the paradox.
Imagine a mouse moving through the grass in front of a tree and in this way producing noise. The owl sitting on a branch of the tree and listening, its ears receive the broad band spectrum produced by the mouse. Vertical sound localization is achieved by measuring the intensity difference between the two ears, which are slightly different, both in position and in feather screening. We have concentrated on horizontal sound localization. It is due to a difference in arrival time between the two ears. Sampling frequencies in the range of two to eight kilohertz (2-8 kHz), the barn owl reaches a precision of two degrees, which is equivalent to detecting an interaural time difference of a few microseconds - amazingly good and, as we already noted, ten to hundred times better than the membrane time constants of the neurons handling the data. How, then, does the owl's brain reach that high a precision?
A brain is made up of many neurons. The essence of a neuron can be described as follows. It consists of three parts: (i) an input part, the dendritic tree, (ii) a central processing unit, that emits a pulse with an amplitude of 0.1 Volt, a so-called spike, when its voltage exceeds a threshold, and (iii) an output part, the axon. The axon is a transmission line for the spikes. At its terminations one finds synapses. These pass spikes to the dendritic tree of another neuron. Synapses play a key role in what follows since their strength can be modified through `learning', a kind of programming that is performed by the system itself.
The first stage of horizontal sound localization is to be accomplished in the so-called laminar nucleus. Here signals from both ears meet. A laminar neuron represents a certain direction in space and, thus, a certain interaural time difference. Its key problem is getting the data from the left and right ear in unison so that they arouse the neuron to fire vigorously. In so doing the neuron would generate spikes but, to this end, it needs enough instantaneous input. The input arrives via the axons coming from other neurons, here from those doing hearing (in the cochlea). A spike traveling along an axon needs a finite amount of time (a delay) to reach a synapse at the axon's termination. The delay varies from axon to axon. Synapses can `learn', however. That is, their efficacy can wax or wane depending on the timing of the arriving spikes in relation to the firing of the receiving neuron - a key element of our theory, as we will see shortly.
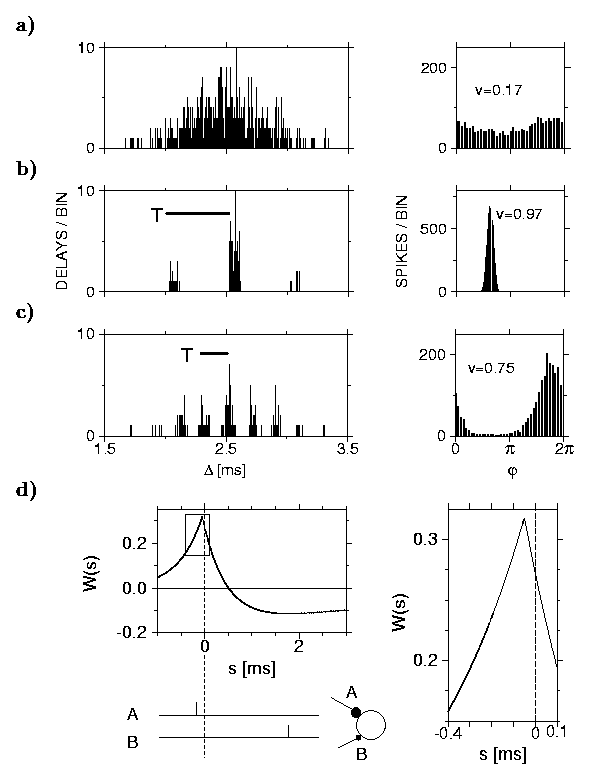
Three weeks after hatching, a barn owl's head has reached its final size but sound localization does not function yet. This is not too surprising in view of a huge scatter of the axonal delays. The scatter blocks a well-tuned periodic arrival of the incoming spikes. To see why, let us consider a 5 kHz signal. This is no restriction since the ears sort out the input according to frequencies. The period is 200 microseconds but, because of the axonal delays, the scatter in the transmission times from the ear to a laminar neuron of a youngster is five times as big; cf. figure (a). The solution to the timing problem is the observation [2] that presumably not genetic coding, which seems implausible in view of many thousands of axons, but a simple training of the synapses at the axon terminations leads to the required fine-tuning.

Figure: (a) Left column: Plot of the delays corresponding to 600 synapses before training. It displays a broad distribution. Right column: The companion plot shows that the neuronal response to a 5 kHz signal is completely smeared out so that sound localization cannot work. (b) & (c) After training only `well-tuned' synapses remain. The input frequencies are (b) 2 kHz and (c) 5 kHz. Synapses that differ by a multiple of the period T (500 and 200 microseconds, respectively) are equally good. The companion plots on the right show a more or less pronounced response. Hence sound localization does work. (d) Plot of the learning window showing the underlying learning process and the relevance of correct timing. Vertically one has the synaptic change W after one learning step and horizontally the spike arrival time s, which either precedes (s < 0) or follows (s > 0) the moment of firing (s = 0) of the postsynaptic neuron, on which the synapses are located. Spikes hitting synapse A arrive slightly before the postsynaptic firing (s < 0) so that A is well-tuned and its efficacy increases, i.e., W(s) > 0. Those at B are too late (s >> 0) and B's strength wanes, i.e., W(s) < 0.
The training singles out synapses and, hence, axons with the right timing; those that differ by a multiple of the period are also fine. The training (doing by hearing) is a kind of selection that is based on the arrival times of incoming spikes as compared to the firing times of the postsynaptic neuron: ``Those that come too late are punished.'' In other words, there is a subtle cooperative process where hundreds of synapses are `steering' a postsynaptic neuron and, in so doing, suppress synapses with the wrong timing but strengthen those that fire in unison with the postsynaptic neuron. The final result of the synaptic learning process is shown in figure (b) and (c). Experimental confirmation [3] of the importance of timing has been provided afterwards; cf. figure (d). It is also known [4] that a youngster's laminar neuron has many more synapses than that of an adult owl, which hints at a selection explained by the present theory. A detailed understanding of the various stages of the underlying cooperative learning process has been attained.
In view of such a successful system performance, one could ponder about applying similar techniques to industrial applications where an extremely good timing in a sensible surroundings is to be realized.
[1] M. Konishi, Scientific American Vol. 268/4, 66 (1993)
[2] W. Gerstner, R. Kempter, J.L. van Hemmen, and H. Wagner, Nature Vol. 383, 76 (1996)
[3] H. Markram, J. Luebke, M. Frotscher, and B. Sakmann, Science Vol. 275, 213 (1997)
[4] C. Carr (University of Maryland), private communication.